The amazing number e

One of the most important numbers we have is a most unusual one also. It is the number we simply refer to as e.

It - like π - goes on forever and does not repeat itself. Its value starts as 2.718281828459045...

The number e is so special because it keeps appearing when we model so many things including growth and decay.

Steps leading to the naming of e.

The first mathematician to find the existence of the constant value e was the Swiss mathematician Jacob Bernoulli (1654 - 1705).

He was investigating the problem of compound interest and so considered the problem of what happens to the value of the expression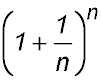
as the number n increases towards infinity. Bernoulli determined that the value of the expression approaches 2.718...

The value of the constant was used by Leonhard Euler (1707-1783) in a number of contexts which expanded our understanding of the real world.
The letter "e" was then given to the number in honour of Euler's many contributions to Mathematics - many of the most important incorporating the value of e.

In 1785, Isaac Newton showed that the series

approached the approximate number (2.718281..)^x when using many, many terms (like an infinite number :-) ) - which was later written as e^x.
When x = 1, this series reduces to that used by Bernouilli.

Ways to calculate the value of e.

As noted above, Bernoulli used 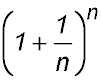which is the same formula we use today for calculating compound interest on an investment.

To test our formula for compound interest therefore, we make up the situation in which we invest $1 at the wonderful rate of interest of 100% (high enough to make any Bank cringe even before a Royal Commission).

If we leave our $1 with the bank for one year, the value of our investment rises to $2 - we double the value of our investment!!! Remember 100% ÷ 100 = 1 for the numerator).

Now we decide a better strategy is to be paid interest TWICE a year on our $1 investment invested for one year - so every 6 months.
. So more money.

What about if we receive our interest three times or four times or five times each year? How much money we will have in our investment?

The following table summarises some of the possibilities:

Investing $1 for one year:
No. of times interest is paid in the year:	Value of the investment after 1 year:
Once	$2.00
twice	$2.25
3 times	$2.37
Quarterly	$2.441
Monthly	$2.613
Daily	$2.714
Each 12 hours	$2.7164
Each hour	$2.7181

Clearly the amount of our investment is approaching a limit - and that limit is e!!!!!!!

Ways to describe e

The constant e can be described in several ways because of it being a number occurring constantly.

In addition to the compound interest application, the number e:

Can be defined as the value for the number a in the exponential equation y = a^x which sets the gradient of the tangent at x = 0 to 1.

y = 2^x	y = e^x	y = 3^x

The above graphs show three exponential graphs:

The graph of y = 2^x: climbs slowest; the tangent has the lowest slope (or gradient) of 0.69 and it cuts the x axis near -1.5.
The graph of y = e^x: climbs evenly, the gradient of the tangent at x = 0 is 1 and it cuts the x axis at -1.
The graph of y = 3^x: climbs the quickest; the tangent has the steepest slope of 1.1 and it cuts the x axis before -1.

The graph with e as its base sets the gradient of the curve - and therefore the gradient of the tangent - to 1 at x = 0. But at x = 0, y = 1.

Hence the function value equals the gradient!!

We can therefore write in symbols: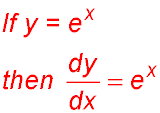

The exponential function with e as its base - f(x) = e^x - is called the natural exponential function.

That result opens up a wide field of differential and integral calculus. It also means that to do calculus with exponential functions -
and with their inverse functions (the logarithmic functions) - the base can only be e.

Logarithmic growth can be regarded as being the opposite of exponential growth